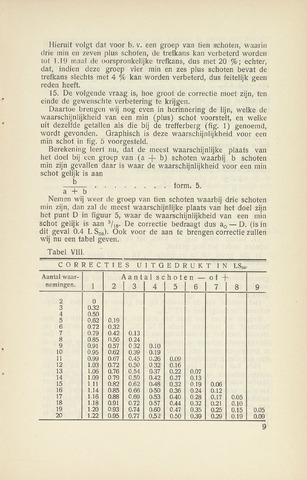
Hieruit volgt dat voor b. v. een groep van tien schoten, waarin
drie min en zeven plus schoten, de trefkans kan verbeterd worden
tot 1.19 maal de oorspronkelijke trefkans, dus met 20 echter,
dat, indien deze groep vier min en zes plus schoten bevat de
trefkans slechts met 4 kan worden verbeterd, dus feitelijk geen
reden heeft.
15. De volgende vraag is, hoe groot de correctie moet zijn, ten
einde de gewenschte verbetering te krijgen.
Daartoe brengen wij nog even in herinnering de lijn, welke de
waarschijnlijkheid van een min (plus) schot voorstelt, en welke
uit dezelfde getallen als die bij de trefferberg (fig. 1) genoemd,
wordt gevonden. Graphisch is deze waarschijnlijkheid voor een
min schot in fig. 5 voorgesteld.
Berekening leert nu, dat de meest waarschijnlijke plaats van
het doel bij een groep van(a -f b) schoten waarbij b schoten
min zijn gevallen daar is waar de waarschijnlijkheid voor een min
schot gelijk is aan
-form. 5.
a b
Nemen wij weer de groep van tien schoten waarbij drie schoten
min zijn, dan zal de meest waarschijnlijke plaats van het doel zijn
het punt D in figuur 5, waar de waarschijnlijkheid van een min
schot gelijk is aan 3/,0. De correctie bedraagt dus aQ D. (is in
dit geval 0.4 L S50). Ook voor de aan te brengen correctie zullen
wij nu een tabel geven.
Tabel VIII.
CORRECTIES UITGEDRUKT IN LS50-
Aantal waar
A a n t
a 1 s c
h o t e n
of H
nemingen.
1
2
3
4
5
6
7
8
9
9
2
0
3
0.32
4
0.50
5
0.62
0.19
6
0.72
0.32
7
0.79
0.42
0.13
8
0.85
0.50
0.24
9
0.91
0.57
0 32
0.10
10
0.95
0.62
0.39
0.19
11
0.99
0.67
0.45
0.26
0.09
12
1.03
0.72
0.50
032
0.16
13
1.06
0.76
0.54
0-37
0.22
0.07
14
1.09
079
0.59
0.42
0.27
0.13
15
1.11
0.82
0.62
0.48
0.32
0.19
0.06
16
1.14
0.85
0.66
0-50
0.36
0.24
0.12
17
1.16
0.88
0.69
0-53
0.40
0.28
0.17
0.05
18
1.18
0.91
0.72
0-57
0.44
0.32
0.21
0.10
19
1.20
0.93
0.74
0.60
0.47
0.35
0.25
0.15
0.05
20
1.22
0.95
0.77
0.52
0.50
0.39
0.29
0.19
0.09